DP 개념
[알고리즘 공부] 다이나믹 프로그래밍(DP, 동적 계획법)
다이나믹 프로그래밍(Dynamic Programming) 하나의 문제를 단 한번만 풀도록 하는 알고리즘 컴퓨터적인 사고력을 물어보기 적합해서 자주 출제되므로 확실하게 알아야 함. DP, 동적 계획법이라고도 함
coding-maggot.tistory.com
11726 2xn 타일링 1
문제
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.
아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.

입력
첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)
출력
첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.
풀이
i) n이 1일 때(2x1) : 2x1 타일 1개 - 1가지
ii) n이 2일 때(2x2) : 2x1 타일 2개 | 1x2 타일 2개 - 2가지
iii) n이 3일 때(2x3) : 2x1 타일 1개 + 1x2 타일 2개 | 1x2 타일 2개 + 2x1 타일 1개 | 2x1 타일 3개 - 3가지
규칙) 앞의 가로 길이가 n-1일 때 맨 끝에 2x1 타일 1개가 오는 것과,
앞의 가로 길이가 n-2일 때 맨 끝에 1x2 타일 2개가 오는 것. 2가지로 나눌 수 있다.
즉, D[n] = D[n-1] + D[n-2] 인 점화식을 세울 수 있고, 메모이제이션을 사용하는 DP를 적용할 수 있다.
#include <stdio.h>
int d[1001];
int dp(int x) {
if(x == 1) return 1;
if(x == 2) return 2;
if(d[x] != 0) return d[x];
return d[x] = (dp(x-1) + dp(x-2)) % 10007;
}
int main() {
int x;
scanf("%d", &x);
printf("%d", dp(x));
return 0;
}
11727 2xn 타일링 2
문제
2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.
아래 그림은 2×17 직사각형을 채운 한가지 예이다.

입력
첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)
출력
첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.
풀이
규칙) 앞의 가로 길이가 n-1일 때 맨 끝에 2x1 타일 1개가 오는 것,
앞의 가로 길이가 n-2일 때 맨 끝에 2x2 타일 1개가 오는 것,
앞의 가로 길이가 n-2일 때 맨 끝에 1x2 타일 2개가 오는 것. 3가지로 나눌 수 있다.
점화식: D[n] = D[n-1] + 2 * D[n-2]
#include <stdio.h>
int d[1001];
int dp(int x) {
if (x==1) return 1;
if (x==2) return 3;
if (d[x] != 0) return d[x];
return d[x] = (dp(x-1) + 2*dp(x-2)) % 10007;
}
int main() {
int x;
scanf("%d", &x);
printf("%d", dp(x));
return 0;
}
2133 3xn 타일링
문제
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
입력
첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.
출력
첫째 줄에 경우의 수를 출력한다.
힌트
아래 그림은 3×12 벽을 타일로 채운 예시이다.
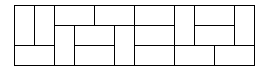
풀이
길이가 1, 3인 경우: 빈 곳이 생기기 때문에 불가능
길이가 2인 경우: 3가지 => D[n] = 3*D[n-2] (미완)
길이가 4인 경우: 2가지
길이가 짝수인 경우에 대해 2가지씩 특별한 케이스가 존재하게 됨
즉, 점화식은
D[n] = 3*D[n-2] + 2*(D[n-4] + D[n-6] + … + D[0])
#include <stdio.h>
int d[30];
int dp(int x)
{
// for문에서 dp(0)일 때 result에 2*dp(0), 즉 2 씩 누적되려면 필요
if (x == 0) return 1;
if (x == 1) return 0;
if (x == 2) return 3;
if (d[x] != 0) return d[x];
int result = 3 * dp(x-2);
for (int i = 2; 2 * i <= x; i++) {
result += 2 * dp(x - 2 * i);
}
// for (int i = 3; i <= x; i++) {
// if(i % 2 == 0) result += 2 * dp(x - i);
// }
return d[x] = result;
}
int main()
{
int x;
scanf("%d", &x);
printf("%d", dp(x));
return 0;
}
14852 2xn 타일링
문제
2×N 크기의 벽을 2×1, 1×2, 1×1 크기의 타일로 채우는 경우의 수를 구해보자.
입력
첫째 줄에 N(1 ≤ N ≤ 1,000,000)이 주어진다.
출력
첫째 줄에 경우의 수를 1,000,000,007로 나눈 나머지를 출력한다.
풀이
길이가 1인 경우: 2가지
길이가 2인 경우: 7가지
그 이후에는 특수한 경우 2가지씩 생김
D[n] = 2*D[n-1] + 3*D[n-2] + 2*(D[n-3]+D[n-4]+...+D[0])
1차원으로 처리하면 데이터가 많아서 시간 초과 뜸… 2차원 dp 적용 필요
| 경우의 수 | 0 | 2 | 7 | 22 | 71 |
| 특수한 고유값 (2를 곱하기 전) |
1 | 1 | 3 |
2씩 고유한 경우가 추가되는 것을 감안하기 위해
바로 앞에 있는 고유값과 3개 앞에 있는 경우의 수를 더한 값을 2차원 행에 기록하고, 2를 곱해 더하는 것
=> 앞에 있는 값 읽어서 처리하므로 시간복잡도가 O(n)밖에 안됨.
// 점화식: D[n] = 2*D[n-1] + 3*D[n-2] + 2*(D[n-3]+D[n-4]+...+D[0])
// 1차원 : 시간 초과 코드
// #include <stdio.h>
// int d[1000001];
// int dp(int x) {
// if (x==0) return 1;
// if (x==1) return 2;
// if (x==2) return 7;
// if (d[x] != 0) return d[x];
// int result = 2*dp(x-1) + 3*dp(x-2);
// for(int i=3; i<=x; i++) {
// result += 2*dp(x-i) & 1000000007;
// }
// return d[x] = result % 1000000007;
// }
// 2차원 dp 적용
#include <stdio.h>
long long d[1000001][2];
long long dp(int x)
{
d[0][0] = 0;
d[1][0] = 2;
d[2][0] = 7;
d[2][1] = 1;
for (int i = 3; i <= x; i++)
{
d[i][1] = (d[i - 3][0] + d[i - 1][1]) % 1000000007;
d[i][0] = (2 * d[i - 1][0] + 3 * d[i - 2][0] + 2 * d[i][1]) % 1000000007;
}
return d[x][0];
}
int main()
{
int x;
scanf("%d", &x);
printf("%lld", dp(x));
return 0;
}
'[C_C++]코딩테스트 연습 > [백준] 일반 문제' 카테고리의 다른 글
| [백준] 그리디 기초 문제풀이 ② - 1138, 1541, 10610, 1946 (C/C++) (1) | 2022.08.20 |
|---|---|
| [백준] 그리디 기초 문제풀이 ① - 5585, 11047, 11399, 2217 (C언어) (0) | 2022.08.20 |
| [백준] 10699 오늘 날짜(C언어) (0) | 2022.07.24 |
| [백준] 삼성 SW 역량 테스트 기출 - 2048 (Easy) (C언어) (0) | 2022.07.20 |
| [백준] 삼성 SW 역량 테스트 기출 - 구슬탈출2 (C언어) (0) | 2022.07.19 |
![[백준] 11726, 11727, 14852 2xn 타일링, 2133 3xn 타일링 (C, DP)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FZ2C53%2FbtrJlPItGLp%2FAAAAAAAAAAAAAAAAAAAAAGmXg1HbIOx-IgfJKXyLBTsp8MOk2a9KQokf6xOPr1YP%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1761922799%26allow_ip%3D%26allow_referer%3D%26signature%3DPCfSIIMIRTGKpqL8qNyWsB1Imf0%253D)