728x90
이진트리(Binary Tree)
- 가장 많이 사용되는 비선형 자료구조
- 트리 자료구조를 활용한 대표적인 예시
- 데이터의 탐색 속도 증진을 위해 사용하는 구조
트리를 제대로 구현하기 위해서는 포인터를 사용해야 함.
포인터를 사용하면 특정한 root에서 자식 노드로 접근하는게 훨씬 간단하게 이루어질 수 있음.
힙 정렬을 구현할 때는 완전 이진 트리를 사용했기 때문에 배열로 표현할 수 있었지만, 완전 이진 트리가 아닌 이진 트리는 배열로 표현하기 어렵기 때문(∵ 데이터 낭비. 오른쪽으로만 뻗는 트리의 인덱스를 생각해 볼 것).
이진 트리에서 데이터를 탐색하는 법 3가지
- 전위 순회(Preorder Traversal)
① 먼저 자기 자신을 처리
② 왼쪽 자식 방문
③ 오른쪽 자식 방문 - 중위 순회(Inorder Traversal)
① 왼쪽 자식 방문
② 먼저 자기 자신을 처리
③ 오른쪽 자식 방문 - 후위 순회(Postorder Traversal)
① 왼쪽 자식 방문
② 오른쪽 자식 방문
③ 먼저 자기 자신을 처리
* 계산기와 같이 수식을 컴퓨터가 계산하기 좋은 형태로 데이터를 바꾸고자 할 때 후위 순회가 많이 사용됨.
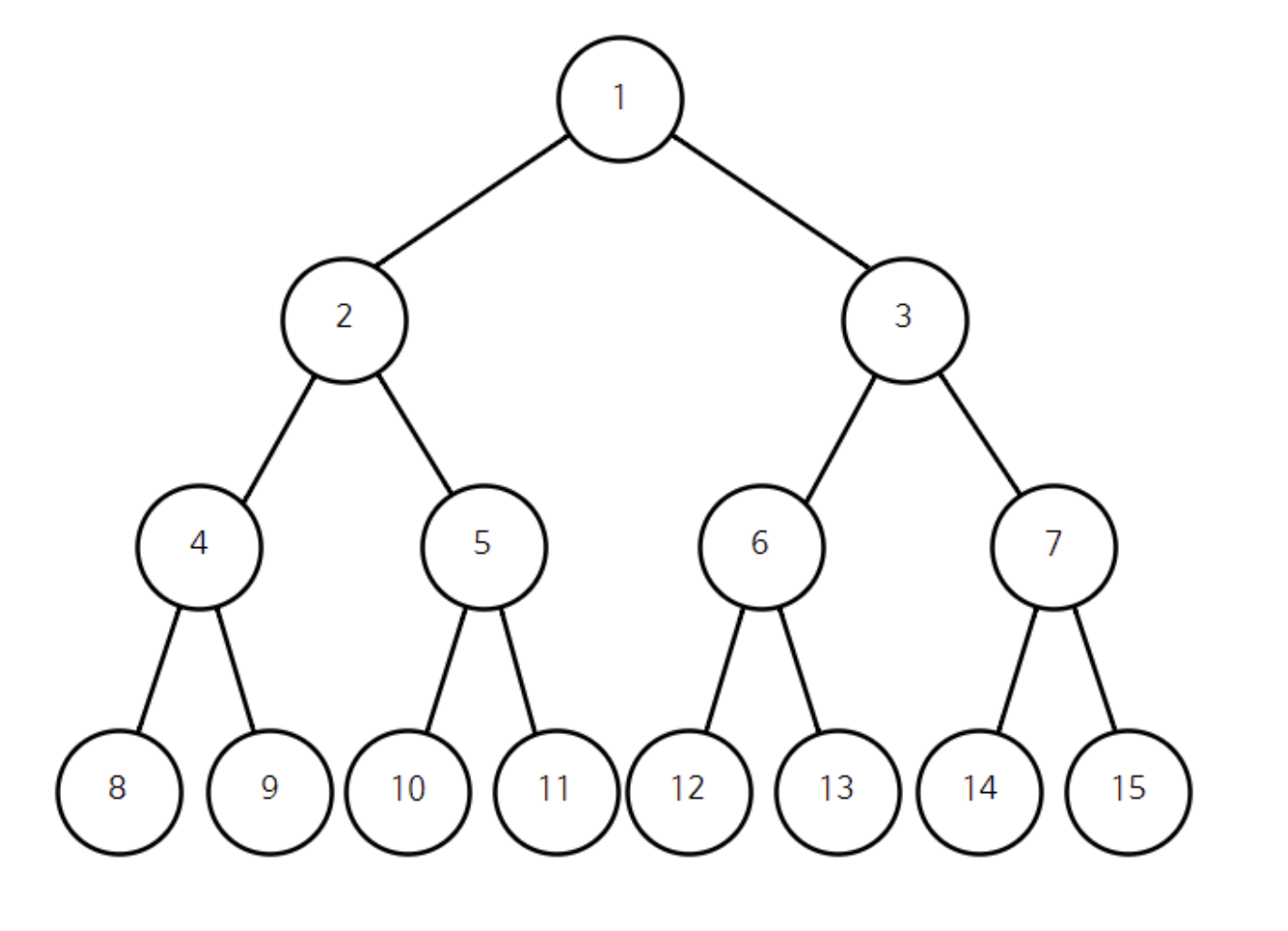
전위 순회: 1 2 4 8 9 5 10 11 3 6 12 13 7 14 15
중위 순회: 8 4 9 2 10 5 11 1 12 6 13 3 14 7 15
후위 순회: 8 9 4 10 11 5 2 12 13 6 14 15 7 3 1
#include <iostream>
using namespace std;
int number = 15;
// 하나의 노드 정보를 선언한다.
typedef struct node *treePointer;
typedef struct node {
int data;
treePointer leftChild, rightChild;
} node;
// 전위 순회 구현
void preorder(treePointer ptr) {
if (ptr) {
cout << ptr->data << ' ';
preorder(ptr->leftChild);
preorder(ptr->rightChild);
}
}
// 중위 순회 구현
void inorder(treePointer ptr) {
if (ptr) {
inorder(ptr->leftChild);
cout << ptr->data << ' ';
inorder(ptr->rightChild);
}
}
// 후위 순회 구현
void postorder(treePointer ptr) {
if (ptr) {
postorder(ptr->leftChild);
postorder(ptr->rightChild);
cout << ptr->data << ' ';
}
}
int main() {
node nodes[number + 1];
// 노드 생성
for (int i = 1; i <= number; i++) {
nodes[i].data = i;
nodes[i].leftChild = NULL;
nodes[i].rightChild = NULL;
}
// 연결
for (int i = 1; i <= number; i++) {
// 짝수면 부모의 왼쪽 자식, 홀수면 오른쪽 자식
if (i % 2 == 0) {
nodes[i / 2].leftChild = &nodes[i];
}
else {
nodes[i / 2].rightChild = &nodes[i];
}
}
// preorder(&nodes[1]);
// inorder(&nodes[1]);
postorder(&nodes[1]);
return 0;
}
'[C_C++]이론 공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘 공부] 에라토스테네스의 체 (0) | 2022.08.18 |
|---|---|
| [알고리즘 공부] 다이나믹 프로그래밍(DP, 동적 계획법) (0) | 2022.08.10 |
| [알고리즘 공부] 합집합 찾기(Union-Find), 크루스칼 알고리즘 (0) | 2022.08.09 |
| [알고리즘 공부] BFS & DFS (C++) (0) | 2022.08.08 |
| [알고리즘 공부] 힙 정렬, 계수 정렬 (C언어) (0) | 2022.08.06 |
![[알고리즘 공부] 이진트리의 구현과 순회 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FlVSdD%2FbtrJWNhBqmF%2FAAAAAAAAAAAAAAAAAAAAAGVvlflreWZbRKMPIw4KEc0MkB5wYZtzW49-nV_3aXjd%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3D7pj1lU2S47IpyruE6XHRDzJd4M4%253D)