다익스트라(Dijkstra) 알고리즘
- DP(다이나믹 프로그래밍)을 활용한 대표적인 최단경로 탐색 알고리즘
최단 거리는 여러 개의 최단 거리로 이루어져 있기 때문에 DP로 분류 가능 (그리디로 분류되기도 함)
하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용 - 현재까지 알고 있던 최단경로를 계속해서 갱신
- 음의 간선을 포함할 수 없음.
- 현실 세계에서 사용하기 매우 적합한 알고리즘 중 하나 (∵ 현실세계에서도 음의 간선이 존재하지 않으므로)
작동 과정
1. 출발 노드 설정
2. 출발 노드 기준으로 각 노드의 최소 비용 저장
3. 방문하지 않은 노드 중 가장 비용이 적은 노드 선택
4. 해당 노드를 거쳐서 특정 노드로 가는 경우를 고려해 최소 비용 갱신
5. 3~4 반복

이러한 그래프는 컴퓨터에서 처리할 때 이차원 배열 형태로 처리해야 함.
- 1번 노드만 보기(1행의 초기 상태)
| 0 | 2 | 5 | 1 | ∞ | ∞ |
현재 방문하지 않은 노드 중 가장 비용이 적은 4번 노드 방문
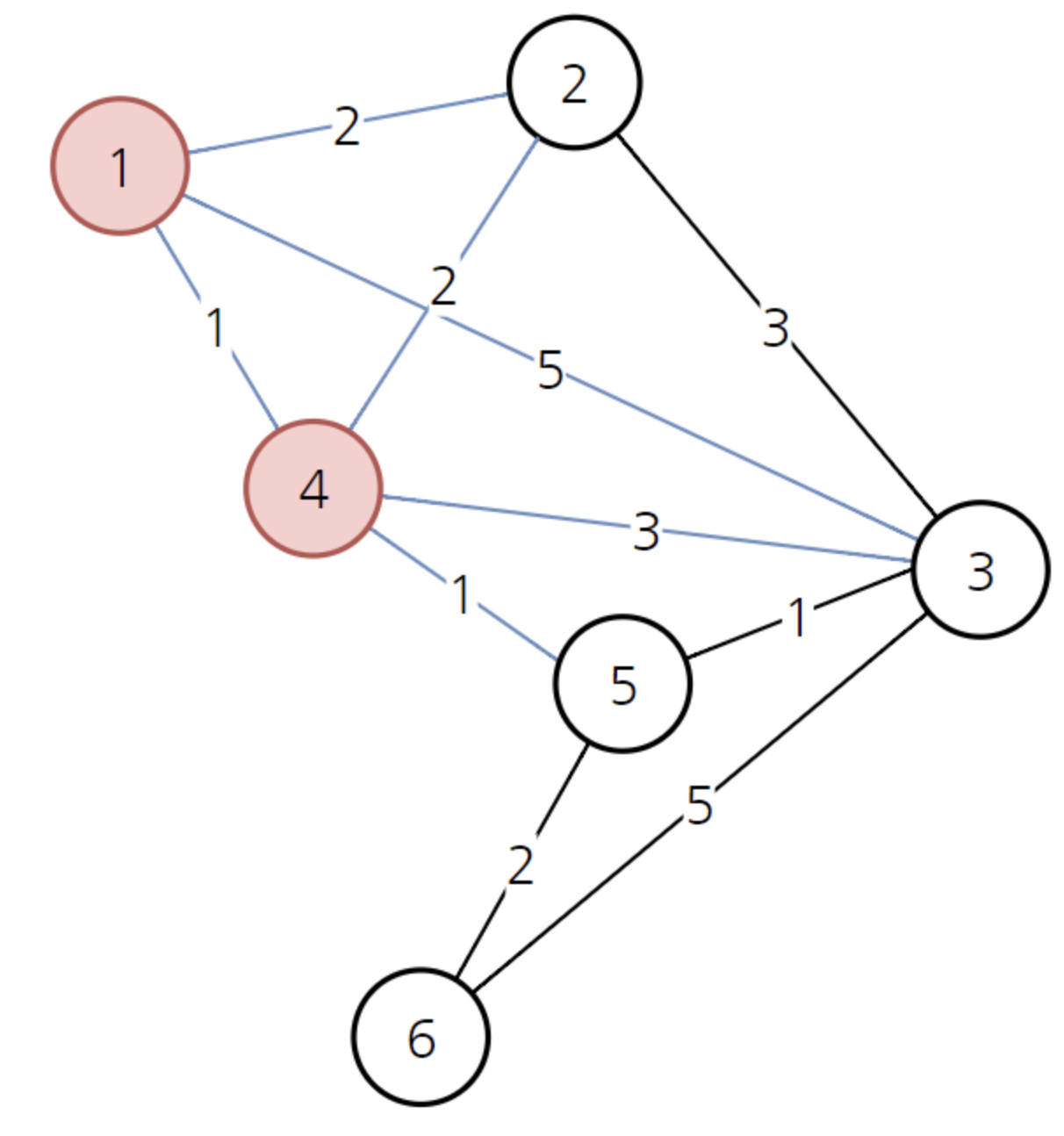
- 4번 노드 방문 후 최소 비용 배열 갱신
| 0 | 2 | 4 | 1 | 2 | ∞ |
이제 방문하지 않은 노드 중 가장 비용이 적은 2번 노드 방문
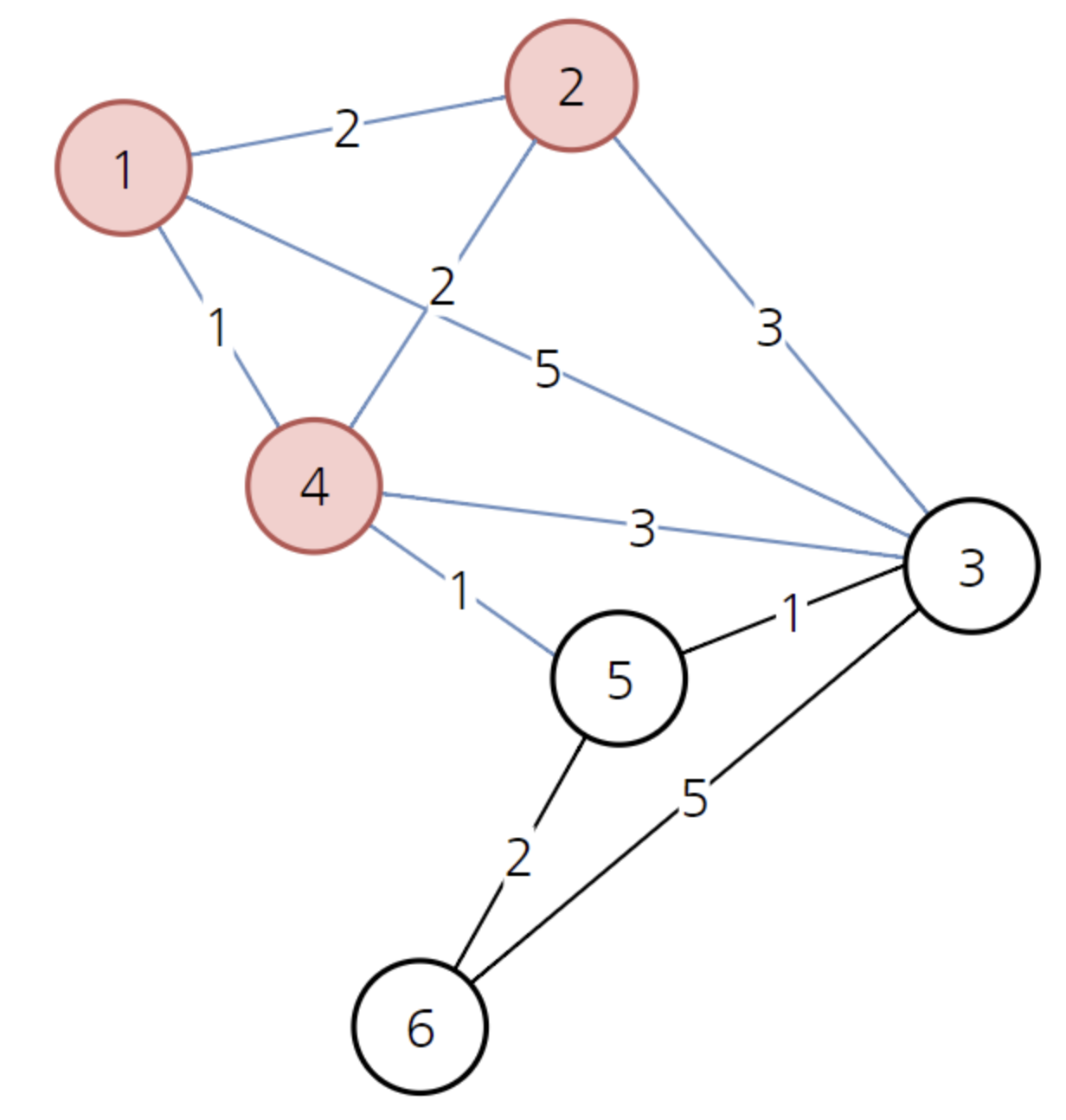
- 2번 노드 방문 후 최소 비용 배열 갱신
| 0 | 2 | 4 | 1 | 2 | ∞ |
이제 방문하지 않은 노드 중 가장 비용이 적은 5번 노드 방문

- 5번 노드 방문 후 최소 비용 배열 갱신
| 0 | 2 | 3 | 1 | 2 | 4 |
이제 방문하지 않은 3번, 6번 노드 방문 후 배열 갱신(변화 X)
| 0 | 2 | 3 | 1 | 2 | 4 |
=> 1번 노드에서의 최단거리인 1행 계산 종료.
다른 노드들도 이런 식으로 하면 됨.
선형 탐색 코드(느림)
#include <stdio.h>
int number = 6;
int INF = 1000000000;
// 전체 그래프 초기화
int a[6][6] = {
{0, 2, 5, 1, INF, INF},
{2, 0, 3, 2, INF, INF},
{5, 3, 0, 3, 1, 5},
{1, 2, 3, 0, 1, INF},
{INF, INF, 1, 1, 0, 2},
{INF, INF, 5, INF, 2, 0},
};
bool v[6]; // 방문 노드
int d[6]; // 거리
// 가장 최소 거리를 가지는 정점을 반환
// 선형 탐색 - 가장 쉽게 다익스트라를 구현하는 방법
int getSmallIndex() {
int min = INF;
int index = 0;
for(int i=0; i<number; i++) {
if(d[i] < min && !v[i]) {
min = d[i];
index = i;
}
}
return index;
}
// 다익스트라를 수행하는 함수
void dijkstra(int start) {
for(int i=0; i<number; i++) {
d[i] = a[start][i];
}
v[start] = true;
for(int i=0; i<number-2; i++) {
int current = getSmallIndex();
v[current] = true;
for(int j=0; j<6; j++) {
if(!v[j]) {
// 현재까지 노드의 최소 거리 + 현재 노드를 거쳐 j로 가는 거리
if(d[current] + a[current][j] < d[j]) {
d[j] = d[current] + a[current][j];
}
}
}
}
}
int main() {
dijkstra(0);
for(int i=0; i<number; i++) {
printf("%d ", d[i]);
}
return 0;
}
선형 탐색으로 최단 거리를 찾으면 시간 복잡도가 O(N^2)로 형성되므로, 실제로는 선형 탐색으로 다익스트라를 구현하면 안 됨.
특히 위와 같은 코드는 정점의 개수가 많은데 간선은 적을 때 치명적일 정도로 비효율적일 수 있음.
다익스트라를 빠른 시간 내에 구현해야하는 상황에 사용하거나, 작동법을 이해하기 위해서만 참고할 것.
=> 힙 구조를 활용해 시간복잡도 O(N*logN) 만들기.
힙 구조 활용 코드
- c++ 에서 제공하는 우선순위 큐를 사용하면 내부적으로 힙과 같은 방식으로 작동
=> 따로 구현할 필요 없이 손쉽게 힙 사용 가능.
- a[]에 간선 정보 저장 : 노드마다 자신과 연결된 노드와 간선비용을 pair 형태로 저장할 수 있게 함.
인접 리스트 방식을 활용해 시간복잡도 O(N*logN) 구현.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int number = 6;
int INF = 1000000000;
vector<pair<int, int>> a[7]; // 간선 정보
int d[7]; // 최소 비용
void dijkstra(int start) {
d[start] = 0;
priority_queue<pair<int, int>> pq; // 힙 구조
// 가까운 순서대로 처리하므로 큐 사용
pq.push(make_pair(0, start));
while (!pq.empty()) {
int current = pq.top().second; // 현재 방문 노드
// 우선순위 큐는 더 큰 값을 기준으로 최상단 노드를 만드는 최대 힙.
// 짧은 것이 먼저 오도록 음수화(-)
// 최상단 노드에 최소 비용이 가장 적은 노드가 담겨있음.
int distance = -pq.top().first;
pq.pop();
// 최단 거리가 아닌 경우 스킵
if (d[current] < distance) continue;
for (int i = 0; i < a[current].size(); i++) {
// 선택된 노드의 인접 노드
int next = a[current][i].second;
// 선택된 노드 거쳐서 인접 노드로 가는 비용
// 선택된 노드까지 가는 최소 비용 + 선택된 노드에서 인접 노드로 가는 비용
int nextDistance = distance + a[current][i].first;
// 기존의 최소 비용보다 더 저렴하다면 교체
if (nextDistance < d[next])
{
d[next] = nextDistance;
pq.push(make_pair(-nextDistance, next));
}
}
}
}
int main()
{
// 기본적으로 연결되지 않은 경우 비용은 무한
for (int i = 1; i <= number; i++)
d[i] = INF;
a[1].push_back(make_pair(2, 2));
a[1].push_back(make_pair(5, 3));
a[1].push_back(make_pair(1, 4));
a[2].push_back(make_pair(2, 1));
a[2].push_back(make_pair(3, 3));
a[2].push_back(make_pair(2, 4));
a[3].push_back(make_pair(5, 1));
a[3].push_back(make_pair(3, 2));
a[3].push_back(make_pair(3, 4));
a[3].push_back(make_pair(1, 5));
a[3].push_back(make_pair(5, 6));
a[4].push_back(make_pair(1, 1));
a[4].push_back(make_pair(2, 2));
a[4].push_back(make_pair(3, 3));
a[4].push_back(make_pair(1, 5));
a[5].push_back(make_pair(1, 3));
a[5].push_back(make_pair(1, 4));
a[5].push_back(make_pair(2, 6));
a[6].push_back(make_pair(5, 3));
a[6].push_back(make_pair(2, 5));
dijkstra(1);
// 결과 출력
for (int i = 1; i <= number; i++)
{
printf("%d ", d[i]);
}
return 0;
}
※ 방문여부를 체크하지 않아도 되는 이유
우선순위 큐를 사용하면 각 노드에서 다른 노드로 이동할 때 최단 경로로 먼저 이동하게 되고,
최단 경로로 이미 방문했다면 방문 여부와 상관없이 거리만으로도 처리가 가능하기 때문
참고글
23. 다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra) 알고리즘은 다이나믹 프로그래밍을 활용한 대표적인 최단 경로(Shortest Path) 탐...
blog.naver.com
'[C_C++]이론 공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘 공부] 그리디(Greedy) 알고리즘 (0) | 2022.08.19 |
|---|---|
| [알고리즘 공부] 플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2022.08.19 |
| [알고리즘 공부] 에라토스테네스의 체 (0) | 2022.08.18 |
| [알고리즘 공부] 다이나믹 프로그래밍(DP, 동적 계획법) (0) | 2022.08.10 |
| [알고리즘 공부] 이진트리의 구현과 순회 알고리즘 (0) | 2022.08.10 |
![[알고리즘 공부] 다익스트라(Dijkstra) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FdkiFrH%2FbtrJWM5Glsl%2FAAAAAAAAAAAAAAAAAAAAAJ_QLq4YjhYneHzKIRKb1I_m1lDdlNGMs2g0TYCF6DYV%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DIuSsGZRUJORy6O0EE0rAkMfgICQ%253D)