다익스트라 알고리즘
- 한 정점에서 출발했을 때 다른 모든 정점으로의 최단 경로를 구하는 알고리즘 (1 → n의 최단경로)
- 가장 적은 비용을 하나씩 선택해서, 그 적은 비용을 갖는 노드와 인접한 노드로 가는 비용을 계산해 알고리즘을 수행
- 가장 적은 비용을 가지는 노드를 하나씩 꺼내서, 그 노드를 거쳐가는 비용을 확인
플로이드 와샬 알고리즘
- '모든 정점'에서 '모든 정점'으로의 최단 경로를 구하는 알고리즘 (n → n의 최단경로)
- 거쳐가는 정점을 기준으로 최단거리를 구함
- 거쳐가는 노드를 하나씩 설정해서 확인 : 거쳐가는 정점을 반복문의 중심에 있게 함.
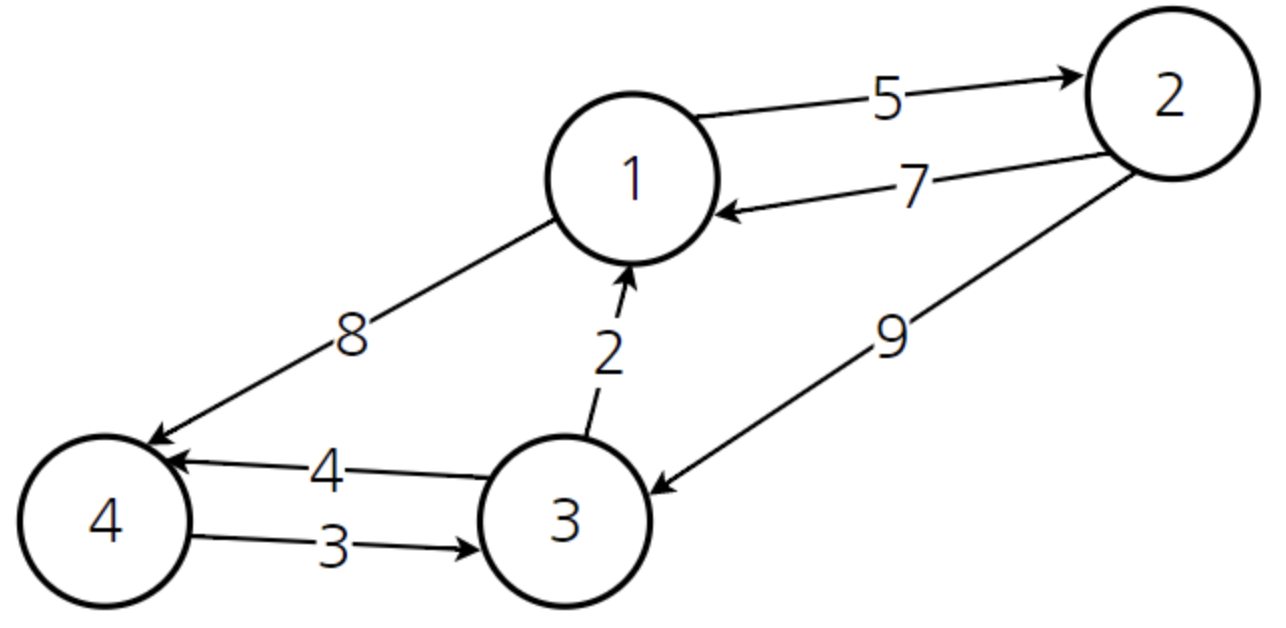
각각의 정점이 다른 정점으로 가는 비용을 이차원 배열 형태로 출력하면
| 0 | 5 | ∞ | 8 |
| 7 | 0 | 9 | ∞ |
| 2 | ∞ | 0 | 4 |
| ∞ | ∞ | 3 | 0 |
=> 현재까지 계산된 최소비용
이러한 2차원 배열을 반복적으로 갱신해 최종적으로 모든 최소 비용을 구해야 함.
반복의 기준 : 거쳐가는 정점
① 노드 1을 거쳐가는 경우
| 0 | 5 | ∞ | 8 |
| 7 | 0 | ||
| 2 | 0 | ||
| ∞ | 0 |
위에서는 6가지 공간만 갱신하면 됨 - 대각선(자기자신으로의 비용 0), a[1][-], a[-][1] 제외
다음의 두 식을 비교해주는 방식을 반복
X에서 Y로 가는 최소 비용 vs X에서 노드 1로 가는 비용 + 노드 1에서 Y로 가는 비용
| 0 | 5 | ∞ | 8 |
| 7 | 0 | (9 vs 2→1→3) 9 |
(∞ vs 2→1→4) 15 |
| 2 | (∞ vs 3→1→2) 7 |
0 | (4 vs 3→1→4) 4 |
| ∞ | (∞ vs 4→1→2) ∞ |
(3 vs 4→1→3) 3 |
0 |
② 노드 2를 거쳐가는 경우
| 0 | 5 | (∞ vs 1→2→3) 14 |
(8 vs 1→2→4) 8 |
| 7 | 0 | 9 | 15 |
| (2 vs 3→2→1) 2 |
7 | 0 | (4 vs 3→2→4) 4 |
| (∞ vs 4→2→1) ∞ |
∞ | (3 vs 4→2→3) 3 |
0 |
이런 식으로 노드 3, 4에 대해서도 수행하면 다음과 같은 결과가 만들어짐.
| 0 | 5 | 11 | 8 |
| 7 | 0 | 9 | 13 |
| 2 | 7 | 0 | 4 |
| 5 | 10 | 3 | 0 |
#include <stdio.h>
int number = 4;
int INF = 100000000;
// 자료 배열 초기화
int a[4][4] = {
{0, 5, INF, 8},
{7, 0, 9, INF},
{2, INF, 0, 4},
{INF, INF, 3, 0}
};
void floydWarshall() {
// 결과 그래프를 초기화
int d[number][number];
for(int i=0; i<number; i++) {
for(int j=0; j<number; j++) {
d[i][j] = a[i][j];
}
}
// k = 거쳐가는 노드
for(int k=0; k<number; k++) {
// i = 출발 노드
for(int i=0; i<number; i++) {
// j = 도착 노드
for(int j=0; j<number; j++) {
if (d[i][k] + d[k][j] < d[i][j]) d[i][j] = d[i][k] + d[k][j];
}
}
}
// 결과 출력
for(int i=0; i<number; i++) {
for(int j=0; j<number; j++) {
printf("%d ", d[i][j]);
}
printf("\n");
}
}
int main() {
floydWarshall();
return 0;
}
- 매우 쉽고 직관적인 알고리즘
- 거쳐가는 노드를 중심으로 포문 전개
- 3중포문을 사용하기 때문에 시간복잡도 O(N^3)
↓ 출력
0 5 11 8
7 0 9 13
2 7 0 4
5 10 3 0
참고글
24. 플로이드 와샬(Floyd Warshall) 알고리즘
지난 시간에는 다익스트라(Dijkstra) 알고리즘에 대해 학습했습니다. 다익스트라 알고리즘은 하나의 정점...
blog.naver.com
'[C_C++]이론 공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘 공부] 그리디(Greedy) 알고리즘 (0) | 2022.08.19 |
|---|---|
| [알고리즘 공부] 다익스트라(Dijkstra) 알고리즘 (0) | 2022.08.19 |
| [알고리즘 공부] 에라토스테네스의 체 (0) | 2022.08.18 |
| [알고리즘 공부] 다이나믹 프로그래밍(DP, 동적 계획법) (0) | 2022.08.10 |
| [알고리즘 공부] 이진트리의 구현과 순회 알고리즘 (0) | 2022.08.10 |
![[알고리즘 공부] 플로이드 와샬(Floyd Warshall) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fbn8zmh%2FbtrJ5xTxSJr%2FAAAAAAAAAAAAAAAAAAAAADCgw28rOITeInM9UaVp7roXhmb37O-T7pMaQeRpJfUJ%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DKhK3tY6ib4EKYDPxw6vxVrQsT8E%253D)